개요
이 문제는 dp와 이분 탐색으로 풀이할 수 있다.
하지만 문제의 입력의 최댓값이 1000이기 때문에 나는 dp로 풀이할 것이다.
dp로 풀이할 때는 이전에 구한 값을 통해 풀이하게 된다.
또한 시간은 O(n^2)이 될 것이다.
문제
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력

풀이
dp[i] = k → i번째 수열까지의 최대 증가수열의 길이 = k 라고 생각하고 접근하면 된다.
예를 들어 수열 {1, 2, 1, 3, 4, 3}이 주어지고 인덱스가 1부터 시작하여 6까지 있다고 생각하면
dp[1] → 1 {1}
dp[2] → 2 {1, 2}
dp[3] → 2 {1, 2}
dp[4] → 3 {1, 2, 3}
dp[5] → 4 {1, 2, 3, 4}
dp[6] → 3 {1, 2, 3}
위와 같이 저장이 될 것이다.
이중 포문을 이용해서 현재 구하는 index → i , 비교대상 index → j 로 생각하고 i 이전의 모든 j에 대해 비교하여 준다.
arr[i] > arr[j] 이고, dp[i] < dp[j] + 1인 경우 dp[i] = dp[j] + 1로 갱신할 것이다.
dp[5]까지 이미 구해져 있다고 가정하고 dp[6]을 구하는 과정은 아래와 같다.


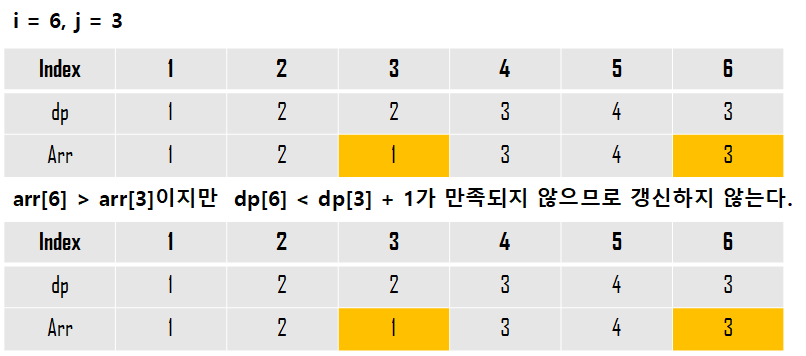
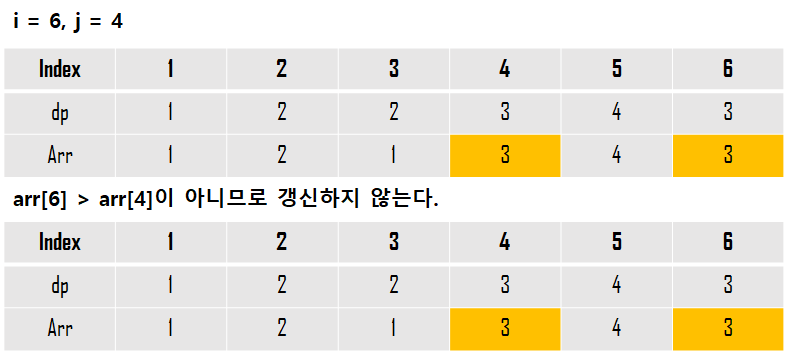

코드
import java.io.*;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static final BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static StringBuilder sb;
public static void main(String[] args) throws IOException {
sb = new StringBuilder();
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n + 1];
int dp[] = new int[n + 1];
// 값의 범위의 최솟값이 1이기 때문에
int result = 0;
StringTokenizer st = new StringTokenizer(br.readLine());
// dp배열 초기화
for(int i = 1; i <= n; i++){
int num = Integer.parseInt(st.nextToken());
// 입력된 배열 값 저장
arr[i] = num;
// 입력된 배열 값과 이전의 값들을 비교한다.
for(int j = 0 ; j < i; j++){
// 비교한 값보다 큰경우
if(arr[i] > arr[j]){
// 비교한 값의 dp값 + 1, 기존의 dp값 중 큰 값을 저장한다.
dp[i] = Math.max(dp[j] + 1, dp[i]);
// 최장 길이인 답을 구하기 위해서 result값에
// 지금까지 구한 dp값 중 가장 큰 값을 저장한다.
result = Math.max(dp[i], result);
}
}
}
// 최장길이 추가
sb.append(result + "\n");
// 최장 길이 값
int value = result;
// 경로를 역추적 할 stack
Stack<Integer> stack = new Stack<>();
// value는 현재 찾는 길이에 해당하는 값이다.
for(int i = n; i >= 1; i--){
// 현재 찾는 길이와 같은 경우
if(value == dp[i]) {
// stack에 실제 값을 push한다.
stack.push(arr[i]);
// 찾는 길이를 찾았으므로 -1을 해주어
// 다음에 찾을 길이를 설정해준다.
value--;
}
}
while (!stack.isEmpty()){
sb.append(stack.pop() + " ");
}
// 출력 버퍼에 write 작업을 한다.
bw.write(sb.toString());
bw.close();
br.close();
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 13913: JAVA] 숨바꼭질 4 / DP, BFS, 역추적 (0) | 2020.03.14 |
|---|---|
| [백준 12738: JAVA] 가장 긴 증가하는 부분 수열 3/ 이분 탐색 (0) | 2020.02.20 |
| [백준 12852: JAVA] 1로 만들기 2 / 동적 프로그래밍 + 역추적 (0) | 2020.02.19 |
| [백준 2482: JAVA] 색상환 / 동적 프로그래밍 (0) | 2020.02.19 |
| [백준 17404: JAVA] RGB거리 2 / 동적 프로그래밍 (0) | 2020.02.19 |



