개요
dp 문제는 이전의 구한 값을 통해 현재 원하는 값을 도출하는 방식이다.
이 문제에서는 중복만 제거한다면 풀이가 가능하다.
또한, 만들고 싶은 금액을 기준으로 한다.
문제
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
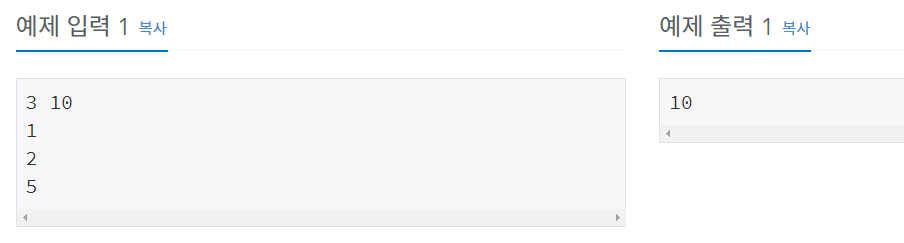
풀이
- dp[] 배열을 선언한다.
- dp[i] = j 라고 하면, 다음과 같다.
- i → 금액
- j → i원을 만드는데 가능한 경우의 수
- dp[i] = dp[i] + dp[i - coin]이다.
- 문제와 같은 입력이 주어졌을 때
- 1원 짜리 동전으로 1원 부터 10원까지 만들 수 있는 가짓수를 구한다.
- 2원 짜리 동전으로 2원 부터 10원까지 만들 수 있는 가짓수를 구한다. (1원으로 구한 값을 이용하여 구한다.)
- 5원 짜리 동전으로 5원 부터 10원까지 만들 수 있는 가짓수를 구한다. (2원으로 구한 값을 이용하여 구한다.)
- 문제와 같은 입력이 주어졌을 때
- 1번 시행시 dp 값
1 2 3 4 5 6 7 8 9 10 (원)
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
- 2번 시행시 dp 값
1 2 3 4 5 6 7 8 9 10 (원)
| 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 |
- 3번 시행시 dp 값
1 2 3 4 5 6 7 8 9 10 (원)
| 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
dp[i] = dp[i - coin] + dp[i] 로 구할 수 있다.
또한 각 동전의 가치부터 인덱스를 잡고 돌리면 중복되는 것을 피할 수 있다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static int n, k;
private static int[] arr, dp;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
arr = new int[n + 1];
dp = new int[k + 1];
dp[0] = 1;
for(int i = 1 ; i <= n; i++) {
arr[i] = Integer.parseInt(br.readLine());
for (int j = arr[i]; j <= k; j++)
dp[j] += dp[j - arr[i]];
}
System.out.println(dp[k]);
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 2606 : JAVA] 바이러스 / BFS (0) | 2020.01.30 |
|---|---|
| [백준 1260 : JAVA] DFS와 BFS / DFS, BFS (0) | 2020.01.30 |
| [백준 7579 : JAVA] 앱 / Dynamic Programming (0) | 2020.01.30 |
| [백준 10942 : JAVA] 펠린드롬? / Dynamic Programming (0) | 2020.01.30 |
| [백준 1655 : JAVA] 가운데를 말해요 / PriorityQueue (2) | 2020.01.26 |



