개요
dp를 이용해서 풀이할 수 있다.
1 2 1 3 1 2 1 수열이 주어졌을 때
dp[][]를 선언하고 dp[i][j]에서 i → 검사하고 싶은 시작 인덱스 j → 검사하고 싶은 끝 인덱스 라고 생각하고 접근한다.
dp문제는 이전에 구한 dp값을 이용해서 현재 원하는 dp값을 구하는 방식이다.
나는 처음에 문제에 접근할 때 시작 점과 끝을 기준으로 dp값을 구하였다.
하지만 이 문제는 길이가 1일 때 펠린드롬인지, 2일 때 펠린드롬인지 ... 을 통해 dp값을 구하면 쉽게 구할 수 있다.
문제
명우는 홍준이와 함께 팰린드롬 놀이를 해보려고 한다.
먼저, 홍준이는 자연수 N개를 칠판에 적는다. 그 다음, 명우에게 질문을 총 M번 한다.
각 질문은 두 정수 S와 E로 나타낼 수 있으며, S번째 수부터 E번째 까지 수가 팰린드롬을 이루는지를 물어보며, 명우는 각 질문에 대해 팰린드롬이다 또는 아니다를 말해야 한다.
예를 들어, 홍준이가 칠판에 적은 수가 1, 2, 1, 3, 1, 2, 1라고 하자.
- S = 1, E = 3인 경우 1, 2, 1은 팰린드롬이다.
- S = 2, E = 5인 경우 2, 1, 3, 1은 팰린드롬이 아니다.
- S = 3, E = 3인 경우 1은 팰린드롬이다.
- S = 5, E = 7인 경우 1, 2, 1은 팰린드롬이다.
자연수 N개와 질문 M개가 모두 주어졌을 때, 명우의 대답을 구하는 프로그램을 작성하시오.
입력
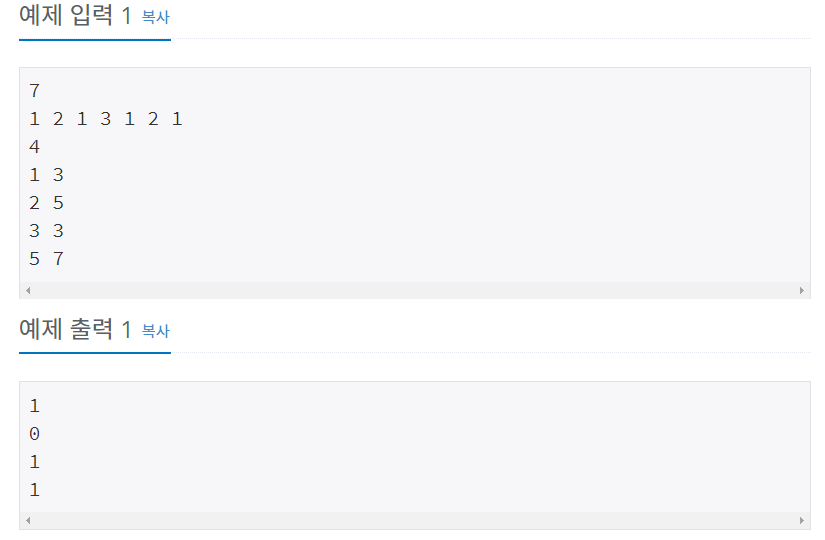
풀이
solve 메소드 부분이 dp배열에 값을 계산하는 부분이고
나머지는 입력을 받고 출력을 하기 위한 코드들이다.
1 2 1 3 1 2 1 수열이 주어졌을 때
- 길이가 1일 경우 → 항상 펠린드롬
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 길이가 2일 경우 → 2개의 수의 값이 같은 경우 펠린드롬
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 1 2 1 3 1 2 1
- 길이가 3이상일 경우 → (시작점 + 1) ~ (끝 - 1) 인덱스 까지 펠린드롬 && 시작점의 값 = 끝의 값 이면 펠린드롬
- 1 2 1 3 1 2 1 → 위 두조건에 만족하므로 펠린드롬
- 1 2 1 3 1 2 1 -> 두 번째 조건을 만족하지 않으므로 펠린드롬이 아니다
- 1 2 1 3 1 2 1 -> 둘 다 만족
- 1 2 1 3 1 2 1 -> 두 번째 조건 만족 x
- 1 2 1 3 1 2 1 -> 둘 다 만족
위의 조건들을 코드로 구현만 하면 된다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static boolean[][] dp;
public static void main(String[] args) throws IOException {
int n = Integer.parseInt(br.readLine());
int []arr = new int[n + 1];
dp = new boolean[n + 1][n + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i = 1 ; i <= n; i++)
arr[i] = Integer.parseInt(st.nextToken());
solve(arr, n);
int m = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i = 0 ; i < m; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
if(dp[start][end]) sb.append("1\n");
else sb.append("0\n");
}
System.out.println(sb);
}
public static void solve(int[] arr, int n){
for(int i = 1; i <= n; i++)
dp[i][i] = true;
for(int i = 1; i <= n - 1; i++)
if(arr[i] == arr[i + 1]) dp[i][i + 1]= true;
for(int i = 2; i < n; i++){
for(int j = 1; j <= n - i; j++){
if(arr[j] == arr[j + i] && dp[j + 1][j + i - 1])
dp[j][j + i] = true;
}
}
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 2293 : JAVA] 동전1 / Dynamic Programming (0) | 2020.01.30 |
|---|---|
| [백준 7579 : JAVA] 앱 / Dynamic Programming (0) | 2020.01.30 |
| [백준 1655 : JAVA] 가운데를 말해요 / PriorityQueue (2) | 2020.01.26 |
| [백준 11286 : JAVA] 절대값 힙 / PriorityQueue (1) | 2020.01.26 |
| [백준 1927 : JAVA] 최소 힙 / PriorityQueue (0) | 2020.01.26 |



