개요
이 문제는 비트 마스크의 기본적인 개념을 활용하면 풀이할 수 있는 문제이다.
처음에는 boolean[]을 선언해서 풀었다.
boolean [20]을 선언하여 b [0] ▶ true이면 1이 있는 것, false이면 1이 없는 것으로 풀이했다.
그러나 문제 이름처럼 bitmask를 이용하면 더욱 메모리를 효율적으로 사용할 수 있다.
int 자료형 a를 선언하면 4바이트(4 * 8bit)를 메모리에 할당받아
총 32개에 대에 참, 거짓을 판단할 수 있게 된다.
a = 00000000 00000000 00000000 00000000(2)로 메모리에 할당받는다.
따라서, 총 0~31까지 수의 집합을 나타낼 수 있다.
2^0자리 ▶ 0의 true, false
2^1자리 ▶ 1의 true, false
2^2자리 ▶ 2의 true, false
...
2^30자리 ▶ 30의 true, false
2^31자리 ▶ 31의 true, false
와 같이 나타낼 수 있다.
문제
비어있는 공집합 S가 주어졌을 때, 아래 연산을 수행하는 프로그램을 작성하시오.
- add x: S에 x를 추가한다. (1 ≤ x ≤ 20) S에 x가 이미 있는 경우에는 연산을 무시한다.
- remove x: S에서 x를 제거한다. (1 ≤ x ≤ 20) S에 x가 없는 경우에는 연산을 무시한다.
- check x: S에 x가 있으면 1을, 없으면 0을 출력한다.
- toggle x: S에 x가 있으면 x를 제거하고, 없으면 x를 추가한다. (1 ≤ x ≤ 20)
- all: S를 {1, 2, ..., 20} 으로 바꾼다.
- empty: S를 공집합으로 바꾼다.
입력
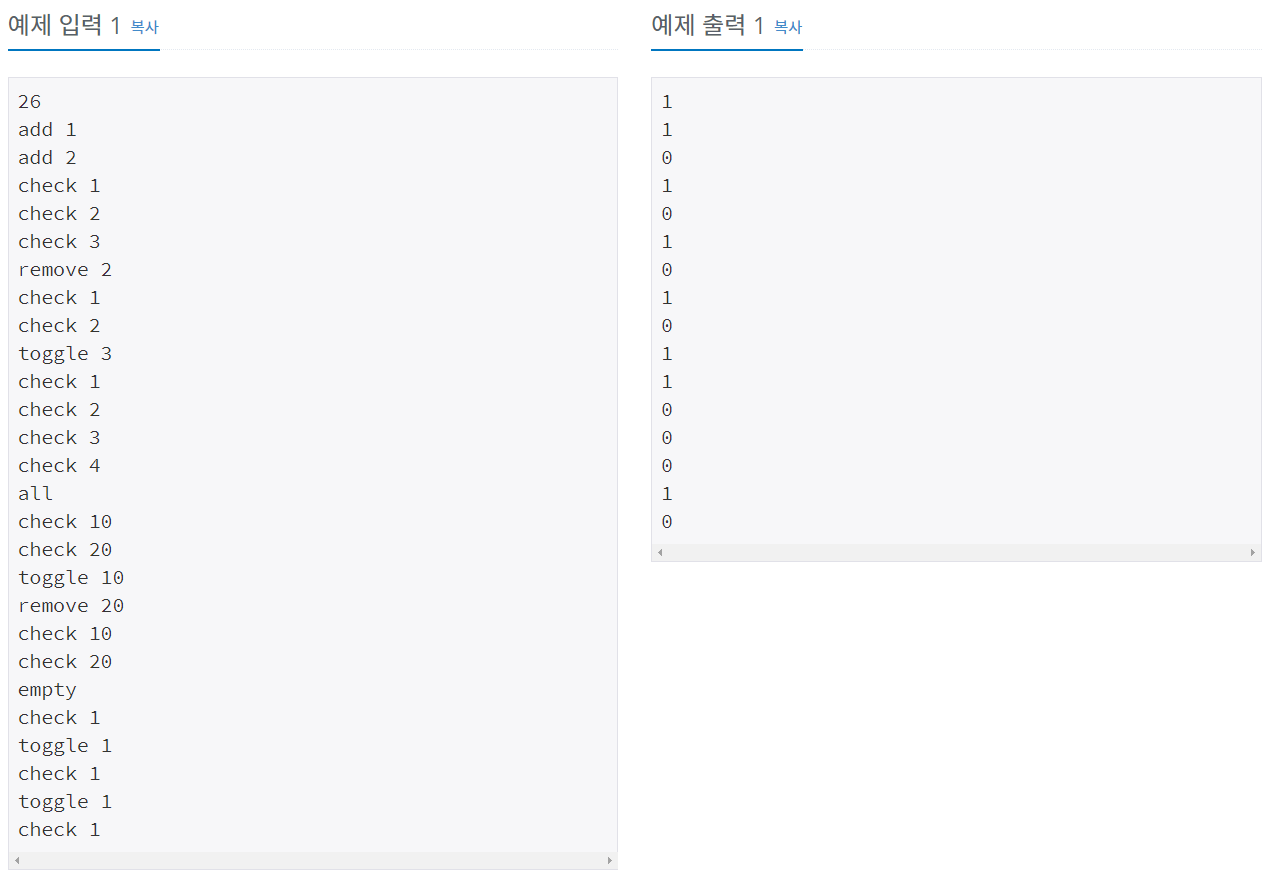
풀이
총 20개의 숫자의 유무를 저장할 수 있어야 하므로 int 자료형 변수 1개면 32개를 표현할 수 있다.
따라서 int 자료형 변수 bitset를 선언하여 풀이할 수 있다.
코드
import java.io.*;
import java.util.StringTokenizer;
// 비트 마스크 문제
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static final BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 출력을 위한 객체
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
int n = Integer.parseInt(br.readLine());
int bitset = 0;
while(n-- > 0){
StringTokenizer st = new StringTokenizer(br.readLine());
String op = st.nextToken();
int num;
// 수행연산
switch (op){
case "add" :
num = Integer.parseInt(st.nextToken());
// num - 1인 이유는 20이 들어왔을 때
// 2^19 자리가 20번째이기 때문이다.
bitset |= (1 << (num - 1));
break;
case "remove" :
num = Integer.parseInt(st.nextToken());
bitset = bitset & ~(1 << (num - 1));
break;
case "check" :
num = Integer.parseInt(st.nextToken());
sb.append((bitset & (1 << (num - 1))) != 0 ? "1\n" : "0\n");
break;
case "toggle" :
num = Integer.parseInt(st.nextToken());
bitset ^= (1 << (num - 1));
break;
case "all" :
bitset |= (~0);
break;
case "empty" :
bitset &= 0;
break;
}
}
bw.write(sb.toString());
bw.close();
br.close();
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준 10815: JAVA] 숫자 카드 / 이분 탐색 (0) | 2020.02.12 |
|---|---|
| [백준 2098: JAVA] 외판원 순회 / dp + 비트 마스크 (0) | 2020.02.12 |
| [백준 1956 : JAVA] 운동 / 벨만-포드 (0) | 2020.02.12 |
| [백준 10217 : JAVA] KCM Travel / 벨만-포드 (0) | 2020.02.12 |
| [백준 11657 : JAVA] 타임머신 / 벨만-포드 (0) | 2020.02.12 |



